Widerstände
Leistungs-, Mess-, Präzisions- und SMD-Widerstände
Ratgeber Widerstände
Inhalt
Wer hat‘s entdeckt?

Georg Simon Ohm, deutscher Physiker: 1789 - 1854
Schon die ersten Experimentatoren in den „Urzeiten“ der Elektrotechnik wussten, dass bei ihren Versuchen immer ein gewisser „Faktor“ im Spiel war, der die „Wirkung der fließenden Elektrizität“ begrenzte. Aber keine der wichtigen elektrischen Größen (heute „elektrische Stromstärke“, „elektrische Spannung“ genannt) konnte exakt gemessen und dieser Zusammenhang schlüssig verstanden werden. Erst Georg Simon Ohm (1789-1854) entwickelte aus seinen Forschungen zur Elektrizität eine grundlegende Theorie, deren Formelwerk bis heute weit verbreitet ist. Damit war die Grundlage geschaffen, um die Zusammenhänge zwischen diesen Größen zu verstehen: Der Widerstand ist einfach das Verhältnis von Spannung und Strom. Damit war es endlich möglich, Widerstandswerte zu berechnen und Bauteile mit definierten Widerstandswerten herzustellen. Dies führte bis heute zu einer unglaublichen Vielfalt von Widerstandsbauformen, die auf den unterschiedlichsten Widerstandstechnologien basieren.
Was ist ein Widerstand?
Der elektrische Widerstand ist im einfachsten Sinne eine Größe, die beschreibt, welchen Strom ein stromdurchflossenes Material bei einer bestimmten Spannung zulässt. Der physikalische Grund für diesen Effekt lässt sich wie folgt erklären: Freie Ladungsträger (Elektronen) werden durch Stöße an Atomen daran gehindert, sich im Leiter frei zu beschleunigen. Das Wort Widerstand (engl. resistor) leitet sich vom lateinischen "resistere" für "widerstehen" ab, was den physikalischen Effekt recht gut beschreibt.
Der Widerstandswert wird in Ohm (Ω) angegeben, das Schaltzeichen ist entweder ein „leeres Rechteck“ nach EN60617 oder hat die Form eines Zickzacks nach ANSI.
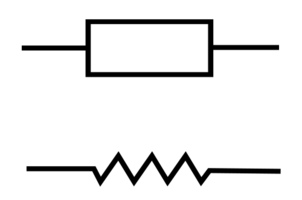
Schaltzeichen für einen elektrischen Widerstand: Rechteck nach EN 60617 oder „Zickzack“ nach ANSI

Ein elektrischer Widerstand im Sinne eines elektronischen Bauelements wird z. B. zur Begrenzung, Messung und Aufteilung elektrischer Ströme verwendet. Grundsätzlich gilt für alle Widerstände, dass das verwendete Material sowie die Dicke und Länge des Widerstandselementes den Stromfluss bestimmen. Der einfachste elektrische Widerstand ist daher ein Stück Draht, obwohl sein Widerstandswert verschwindend gering ist und bei der Berechnung einer Schaltung meist vernachlässigt werden kann.
Der Widerstandswert eines elektrischen Leiters ergibt sich vereinfacht aus dem Quotienten von Spannung und Strom:
R = U / I (R: Widerstand, U: Spannung, I: Strom)
Im Idealfall ist der Widerstandswert konstant, d.h. er ändert sich nicht in Abhängigkeit vom angelegten Strom oder der angelegten Spannung:
R = U / I = const.
In diesem Fall spricht man vom ohmschen Widerstand und der Zusammenhang ist als ohmsches Gesetz bekannt. In der Praxis wird dies bei der Berechnung von Schaltungen meist als gegeben angenommen.
Leider gibt es in der Realität Einflüsse, die den Widerstandswert etwas verändern. Vor allem die Temperatur hat auch bei den besten Widerständen einen gewissen Einfluss auf den Wert, da die Materialien bei Temperaturänderungen ihr Verhalten ändern. Siehe dazu die Erklärung des TK-Wertes weiter unten. Hinzu kommen Rauscheffekte, die ebenfalls die Handhabung elektrischer Schaltungen erschweren (siehe Rauschverhalten von Widerständen). Nicht zuletzt treten Alterungseffekte auf, und hier trennt sich die Spreu vom Weizen.
Rauschverhalten von Widerständen
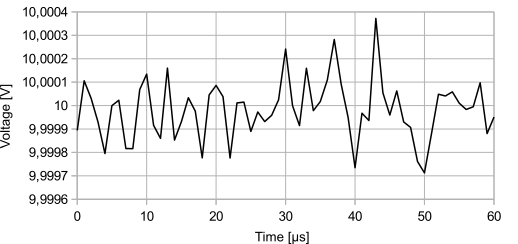
Thermisches Rauschen im Sub-mV-Bereich bei einem Signal von exakt 10 V
Grundsätzlich gibt es zwei Arten von Rauschquellen beim Betrieb von Widerständen:
- Thermisches Rauschen und
- Stromrauschen
Thermisches Rauschen / weißes Rauschen
Thermisches Rauschen ist ein grundlegender physikalischer Effekt, der selbst in einem idealisierten, „theoretischen“ Bauteil auftritt. Es wird auch als „weißes Rauschen“ bezeichnet. Der Effekt verstärkt sich mit steigender Temperatur, und es wird empfohlen, die Temperatur so niedrig wie möglich zu halten, um diesen Rauschanteil zu minimieren. Beim Betrieb mit Wechselspannung hängt das Rauschen auch nicht von der Frequenz, sondern nur von der Messbandbreite ∆f ab. Das weiße Rauschen tritt unabhängig von der angelegten Spannung auf und die Rauschspannung kann wie folgt berechnet bzw. abgeschätzt werden:
\(U_R = \sqrt(4 * k_b * (T_c+273.15) *∆f\)
kb = 1.38*10-23 (Boltzmannkonstante)
TC = Temperatur in °C
R = Widerstandswert
∆f = Bandbreite in Hz (Frequenzbereich, der betrachtet wird)
Für einen Wert von R = 1 MΩ ergibt sich bei einer Bandbreite von ∆f = 20 kHz (Bereich des menschlichen Gehörs) eine Rauschspannung von ca. 0,018 mV bzw. 18 µV.
Dieser Wert ist nicht groß, kann aber bei Anwendungen, bei denen sehr kleine Signale gemessen werden sollen, problematisch sein. Insbesondere in der Audiotechnik ist dieses Rauschen ein ständiger Begleiter der Entwickler hochwertiger Geräte, da prinzipiell alles, was elektrisch leitend ist, Rauschen erzeugt.
Stromrauschen
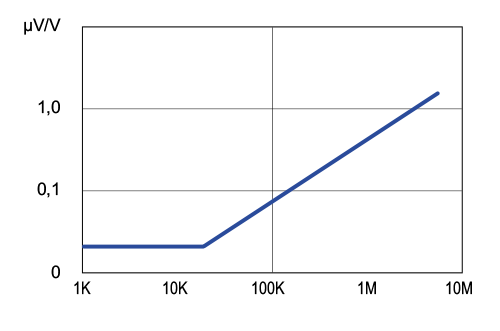
Stromrauschen eines Präzisionswiderstands Serie NC550
Im Gegensatz zum weißen Rauschen tritt das Stromrauschen nur dann auf, wenn an einem Widerstand tatsächlich eine Spannung anliegt. Der durch das Element fließende Strom (der gewünschte Strom) wird durch das Stromrauschen überlagert. Die Ursache des Effekts ist aber gerade der gewünschte Strom, es besteht also eine Abhängigkeit vom Wert des Sollstroms selbst. Hier hängt das Verhalten des Bauelements sehr stark vom verwendeten Widerstandsmaterial ab. Die Einheit für das Stromrauschen wird üblicherweise in µV/V (typischerweise als Maximalwert) angegeben. Das bedeutet, dass dieser Wert einfach mit der Spannung multipliziert werden kann, um den zu erwartenden (maximalen) Rauschpegel zu erhalten. Die Werte hängen vom Widerstandswert selbst ab und sind in der Regel bei höheren Widerstandswerten größer.
Belastbarkeit und Verlustleistung von Widerständen

Leistungsminderungskurve eines Präzisionswiderstands Serie NC550
Widerstände erzeugen Verlustleistung, indem sie elektrische Energie in Wärmeenergie umwandeln. Diese Wärme muss abgeführt werden, um eine Überhitzung des Bauteils zu vermeiden. Die maximalen Temperaturen sind in den Datenblättern angegeben. Bei höherwertigen Modellen finden sich Diagramme, die die Abhängigkeit der maximalen Leistung von der Temperatur zeigen, die Leistungsminderungskurve. Wird die maximal zulässige Temperatur überschritten, nimmt das Bauteil Schaden und kann entweder ganz ausfallen oder seine Eigenschaften verschlechtern oder verändern. Bei Widerständen, die besonders viel Leistung aufnehmen können, wird im Datenblatt angegeben, wie die Wärmeabfuhr zu erfolgen hat. In einigen Fällen gibt es Kühlkörper, die neben Konvektion und Strahlung auch die Wärmeabfuhr durch Kontakt mit einem größeren Kühlkörper erfordern. Je nach Einbausituation können sich die Angaben unterscheiden bzw. es werden Einbauempfehlungen für die verschiedenen Situationen genannt. Die Verlustleistung von Widerständen, d.h. die in Wärme umgewandelte Leistung, berechnet sich bei Gleichstrom zu
P (Leistung) = U (Spannung) *I (Strom).
Bei Wechselstrom werden die Effektivwerte von Strom und Spannung verwendet. Es wird dringend empfohlen, bei der Auswahl des Bauteils nicht zu nahe an die spezifizierten Leistungsgrenzen zu gehen. Ein Widerstand, der im Grenzbereich betrieben wird, erwärmt sich und erwärmt damit auch die Umgebung, was Nebeneffekte auf andere Bauteile haben kann. Diese Nebeneffekte können dazu führen, dass eine mit hochwertigen Bauelementen präzise aufgebaute Schaltung durch diese thermischen Effekte den gesamten Präzisionsvorteil verliert, was das Vorhaben ad absurdum führt. Außerdem hat man kaum Reserven, wenn etwas „schiefgeht“ und die Last höher wird als ursprünglich berechnet. Manchmal kann es sinnvoll sein, zwei Leistungswiderstände parallel zu schalten, um den Einsatz eines einzelnen, meist teureren, leistungsstärkeren Widerstandes zu vermeiden. Wenn in Datenblättern die Temperatur auf die Umgebungsluft bezogen wird, sollte nicht die Raumtemperatur um das Gerät als Referenz genommen werden, sondern die Temperatur, die das Bauteil tatsächlich umströmt (idealerweise Kühlluft). Hier kann der Wert deutlich höher liegen. Sollten dennoch höhere Leistungen erforderlich sein, gibt es Modelle, die Abhilfe schaffen: Einige Widerstandsmodelle erlauben einen gepulsten Betrieb mit kurzzeitig deutlich höherer Belastung. Siehe dazu den Leitfaden für Leistungswiderstände.

Alterungsverhalten / Stabilitätsangaben
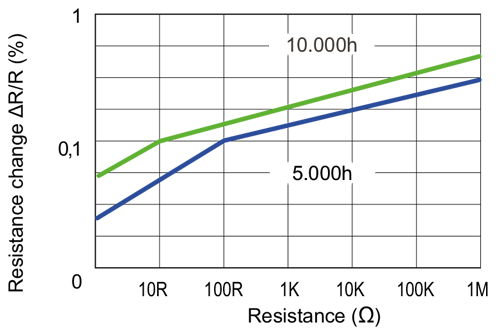
Stabilitätsplot eines Präzisionswiderstands bei einer Leistung von 70 Watt
Grundsätzlich ändern elektrische Widerstände ihren Widerstandswert während der Lebensdauer ohne äußere Einflüsse. Dabei kann es insbesondere zu Beginn der Lebensdauer zu größeren Änderungen kommen als später im Betrieb. Es liegt daher nahe, bei besonderen Anforderungen an die Stabilität den Widerstand in einem beschleunigten Prozess künstlich zu altern. Im Allgemeinen wird in diesem Zusammenhang der Begriff „Stabilität“ verwendet. Bei Präzisionswiderständen findet man in den Datenblättern meist Diagramme, die die Widerstandsänderung bei konstanter (angegebener) Leistung in Abhängigkeit vom Widerstandswert und der Betriebsdauer zeigen.
Widerstände ändern ihre Werte mit der Temperatur. Diese Temperaturabhängigkeit des Gesamtwertes hängt stark von der Bauform und dem verwendeten Material ab. Hinzu kommt, dass der Betrieb des Widerstandes selbst Wärme erzeugt. Um diesen Effekt zu minimieren, muss daher für eine ausreichende Belüftung gesorgt werden. Außerdem wird empfohlen, die Bauelemente nicht in der Nähe der maximal zulässigen Verlustleistung zu betreiben, da gerade in diesem Fall mit einer hohen Eigenerwärmung zu rechnen ist.

Als Maß für die Änderung des Widerstandswertes wird der Temperaturkoeffizient (TK-Wert) angegeben. Der Wert wird in der Einheit ppm / ˚C angegeben (ppm = parts per million, 1 ppm = „1 Millionstel“ des Gesamtwertes).
Wird für einen Widerstand ein TK-Wert von ±50 ppm / °C angegeben, so ändert sich der Widerstand bei einer Temperaturänderung von 1 °C maximal um den multiplikativen Faktor ±0,000050, also um „50 Millionstel“ des Gesamtwertes. Angenommen, ein Bauteil hat einen spezifizierten Widerstandswert von 1 MΩ. Dann kann sich bei einer Temperaturerhöhung oder -senkung um 1 °C der spezifizierte Widerstandswert um bis zu 50 Ω ändern, also um bis zu 50 Ω kleiner oder größer werden. Im Allgemeinen kann folgende Formel verwendet werden
RT=Rref *[1+TK*(T-Tref)]
Wobei
Tref...Referenztemperatur (meist 20°C, manchmal auch 0°C oder 25°C)
Rref...Referenzwiderstand
TK...Temperaturkoeffizient
T... Betriebstemperatur
RT...Widerstandswert im Betrieb
Das gilt für das Beispiel im Text oben:
Tref = 20°C
Rref = 1 MΩ = 1 000 000 Ω
TK = ±50 ppm / °C = ±0,000050 / °C
Die Formel ergibt für die Änderungen von 1°C und 10°C folgende Werte:
R(T=20°C) = 1 MΩ * [1 ± 0,000050 * (20 – 20)] = 1 MΩ * [1 ± 0] = 1 MΩ
R(T=21°C) = 1 MΩ * [1 ± 0,000050 * (21 – 20)] = 1 MΩ * [1 ± 0,000050] = 1 000 000 Ω ± 50 Ω
R(T=40°C) = 1 MΩ * [1 ± 0,000050 * (40 – 20)] = 1 MΩ * [1 ± 0,001000] = 1 000 000 Ω ± 1000 Ω
Wir führen ausschließlich Qualitätswiderstände in unserem Portfolio, die ein deutlich besseres Stabilitäts- und Langzeitverhalten aufweisen und wesentlich engere Widerstandstoleranzen und genauere Widerstandswerte als Standardwiderstände ermöglichen. Unser Schwerpunkt sind Präzisionswiderstände.
Leistungswiderstände, Messwiderstände, Spannungsteiler oder Thermistoren - oft handelt es sich um sehr individuelle und kundenspezifische Bauteile. Mit unserem „Resistor Engineering“ beraten wir Sie gerne und finden für Sie die optimale Produktlösung; und das bereits ab relativ kleinen Stückzahlen.
Wir sind Ihr Partner für qualitativ hochwertige Produkte. Mit hoher Liefertreue setzen wir auf langfristige Partnerschaften und begleiten Sie über den gesamten Lebenszyklus Ihrer Anwendung. Unser Anspruch ist es, jedem Kunden individuell das funktional und wirtschaftlich beste Ergebnis zu liefern. Ein Komplettpaket genau für Ihren Bedarf. Das ist unser Motto seit über 60 Jahren.
 EN
EN DE
DE ES
ES FR
FR PT
PT IT
IT


































