Résistances
Résistances de puissance, de mesure et SMD
Guide des résistances
Contenu
Qui l'a découvert ?

Georg Simon Ohm, physicien allemand : 1789 - 1854
Les premiers expérimentateurs des "premiers temps" de l'électrotechnique savaient déjà que leurs expériences faisaient toujours intervenir un certain "facteur" qui limitait "l'effet de l'électricité en mouvement". Mais on ne pouvait mesurer avec précision aucune des grandeurs électriques importantes (appelées aujourd'hui "intensité du courant électrique", "tension électrique") et comprendre cette relation de manière concluante. Ce n'est que Georg Simon Ohm (1789-1854) qui a développé une théorie fondamentale à partir de ses recherches sur l'électricité, dont les formules sont encore largement utilisées aujourd'hui. La base était désormais posée pour comprendre les relations entre ces grandeurs : La résistance apparaît simplement comme le rapport entre la tension et le courant. Finalement, les valeurs de résistance ont pu être calculées et la fabrication de composants avec des valeurs de résistance définies a été rendue possible. Aujourd'hui encore, cela conduit à un nombre incroyablement élevé de modèles de résistances basés sur les technologies de résistance les plus diverses.
Qu'est-ce qu'une résistance ?
Dans son sens le plus fondamental, la résistance électrique est une grandeur qui décrit le courant qu'un matériau autorise à le traverser à une tension fixée. La raison physique de cet effet peut s'expliquer ainsi : Les porteurs de charge libres (électrons) sont empêchés par des chocs sur les atomes d'être accélérés librement dans le conducteur. Le mot résistance (en anglais resistor) est dérivé du latin "resistere" qui signifie résister, ce qui décrit assez bien l'effet physique. La valeur de la résistance est indiquée en ohms (Ω), le symbole de commutation est soit un "rectangle vide" selon EN60617, soit a la forme d'un zigzag selon ANSI.
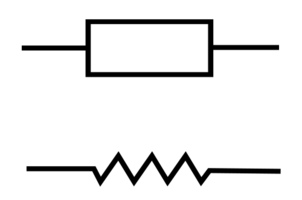
Symbole de commutation pour une résistance électrique : rectangle selon EN 60617 ou "zigzag" selon ANSI

Une résistance électrique, au sens d'un composant électronique, est utilisée pour limiter, mesurer, diviser et bien plus encore les courants électriques. En principe, pour toutes les résistances, le matériau utilisé ainsi que l'épaisseur et la longueur de l'élément résistif déterminent le flux de courant. Un morceau de fil peut donc être considéré comme la résistance électrique la plus simple, bien que sa valeur de résistance soit infinitésimale et puisse généralement être négligée lors du calcul d'un circuit. Pour déterminer la valeur de résistance d'un conducteur électrique, il suffit de diviser la tension électrique par le courant :
R = U / I (R...résistance, U...tension, I...courant).
Idéalement, la valeur de la résistance est constante. Elle ne change donc pas de valeur en fonction du courant ou de la tension qui est appliquée :
R = U / I = const.
Elle est alors également appelée résistance "ohmique" et la relation est connue sous le nom de loi d'Ohm. Dans la pratique, cette loi est généralement considérée comme acquise lors du calcul des circuits.
Malheureusement, dans la réalité, il existe des influences qui modifient quelque peu la valeur de la résistance. Mais c'est surtout la température qui a une certaine influence sur la valeur, même pour les meilleures résistances, car les matériaux changent de comportement en fonction des variations de température. Voir à ce sujet l'explication de la valeur TK ci-dessous. S'y ajoutent des effets de bruit qui compliquent également le traitement des circuits électriques (voir Comportement au bruit des résistances). Enfin, il y a les effets du vieillissement et c'est là que le bon grain se sépare de l'ivraie.
Comportement au bruit des résistances
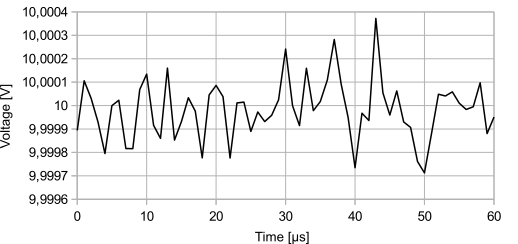
Bruit thermique inférieur à mV pour un signal d'exactement 10 V
En principe, il existe deux types de sources de bruit lors du fonctionnement des résistances :
- Le bruit thermique
- Le bruit de courant
Bruit thermique / bruit blanc
Le bruit thermique est un effet physique fondamental qui se produit même pour un composant idéalisé et "théorique". Il est également appelé "bruit blanc". Cet effet s'accentue avec l'augmentation de la température et il est donc recommandé de maintenir la température la plus basse possible afin de minimiser ce bruit. Lors du fonctionnement en tension alternative, le bruit ne dépend pas non plus de la fréquence, mais uniquement de la largeur de bande de mesure ∆f. Le bruit blanc se produit indépendamment d'une tension appliquée et la tension de bruit peut être calculée ou estimée comme suit :
\(U_R = \sqrt(4 * k_b * (T_c+273.15) *∆f\) kb = 1.38*10-23 (constante de Boltzmann) TC = température en °C R = valeur de la résistance ∆f = largeur de bande en Hz (plage de fréquence considérée).
Pour une valeur de R = 1 MΩ, on obtient une tension de bruit d'environ 0,018 mV ou 18 µV pour une largeur de bande de ∆f = 20 kHz (plage de l'oreille humaine). Cette valeur n'est pas grande, mais elle peut poser problème dans les applications où de très petits signaux doivent être mesurés. Dans la technique audio en particulier, ce bruit est le compagnon permanent des développeurs d'appareils de haute qualité, car en principe, tout ce qui est conducteur d'électricité génère du bruit.
Bruit de courant
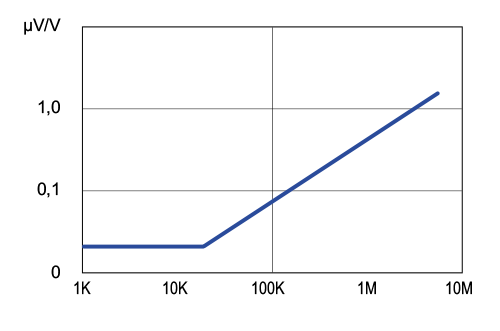
Bruit de courant d'une résistance de précision série NC550
Contrairement au bruit blanc, le bruit de courant n'apparaît que lorsqu'une tension est effectivement appliquée à une résistance. Le courant qui circule dans l'élément (le courant souhaité) est masqué par le bruit de courant. Mais la cause de l'effet se trouve justement dans le courant souhaité, c'est pourquoi il existe une dépendance de la valeur du courant de consigne lui-même. Ici, le comportement de l'élément dépend fortement du matériau de résistance utilisé. L'unité pour le bruit de courant est généralement indiquée en µV/V (typiquement comme valeur maximale). Cela signifie que cette valeur peut simplement être multipliée par la tension et que l'on obtient ainsi le niveau de bruit (maximal) auquel on peut s'attendre. Les valeurs dépendent de la valeur de la résistance elle-même et sont généralement plus élevées pour des valeurs de résistance plus élevées.
Capacité de charge et puissance dissipée des résistances

Courbe de réduction de puissance d'une résistance de précision série NC550
Les résistances génèrent de la puissance dissipée en convertissant l'énergie électrique en énergie thermique. Cette chaleur doit être dissipée afin d'éviter la surchauffe du composant. Les températures maximales sont indiquées sur les fiches techniques. Sur les modèles haut de gamme, on trouve des graphiques montrant la dépendance de la puissance maximale par rapport à la température, la courbe de réduction de puissance. En cas de dépassement de la température maximale autorisée, le composant subit des dommages et peut soit tomber complètement en panne, soit voir ses propriétés se détériorer ou se modifier. Pour les résistances qui peuvent absorber une puissance particulièrement élevée, la fiche technique indique comment la chaleur doit être dissipée. Dans certains cas, il existe des dissipateurs qui, en plus de la convection et du rayonnement, nécessitent également la dissipation de la chaleur par contact avec un dissipateur plus grand. Selon la situation de montage, les indications peuvent différer et les recommandations de montage peuvent être mentionnées pour les différentes situations. La puissance dissipée par les résistances, c'est-à-dire la puissance qui est transformée en chaleur, se calcule en courant continu avec
P (puissance) = U (tension) *I (courant).
Pour le courant alternatif, on utilise les valeurs efficaces du courant et de la tension. Il est fortement recommandé de ne pas choisir un composant trop proche des limites de puissance spécifiées. Une résistance fonctionnant dans la plage limite s'échauffe et réchauffe alors également l'environnement, ce qui peut avoir des effets secondaires sur d'autres composants. Ces effets secondaires peuvent avoir pour conséquence qu'un circuit conçu avec précision avec des composants de haute qualité perde tout l'avantage de la précision à cause de ces effets thermiques, ce qui rend le projet absurde. De plus, on n'a guère de réserves si quelque chose "tourne mal" et que la charge devient plus élevée que celle calculée initialement. Il peut parfois être judicieux de monter deux résistances de puissance en parallèle pour éviter d'utiliser une seule résistance plus puissante et généralement plus chère. Si les fiches techniques indiquent que la température se réfère à l'air ambiant, il ne faut pas prendre comme référence la température ambiante autour de l'appareil, mais la température qui circule effectivement autour du composant (idéalement de l'air de refroidissement). Dans ce cas, la valeur peut être nettement plus élevée. Si, malgré tout, il faut répondre à un besoin de puissance plus élevé, il existe des modèles qui permettent de remédier à cette situation : Certains modèles de résistance permettent un fonctionnement pulsé avec une charge nettement plus élevée pendant une courte période. Voir à ce sujet le guide des résistances de puissance.

Comportement au vieillissement / indications de stabilité
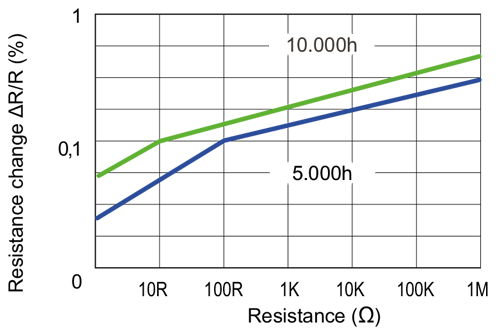
Tracé de stabilité d'une résistance de précision à une puissance de 70 watts
En principe, les résistances électriques changent de valeur au cours de leur durée de vie sans influence extérieure. Dans ce cas, les changements peuvent être plus importants au début de la durée de vie que plus tard pendant le fonctionnement. Il est donc logique, en cas d'exigences particulières en matière de stabilité, de vieillir artificiellement la résistance dans un processus accéléré. En principe, le terme "stabilité" est utilisé dans ce contexte. Pour les résistances de précision, on trouve généralement sur les fiches techniques des graphiques qui montrent la variation de la résistance à puissance constante (indiquée) en fonction de la valeur de la résistance et de la durée de fonctionnement.
Les résistances changent de valeur lorsque la température varie. Cette dépendance de la valeur totale à la température dépend fortement de la forme de construction et du matériau utilisé. À cela s'ajoute le fait que c'est justement le fonctionnement de la résistance elle-même qui génère de la chaleur. Pour minimiser cet effet, il faut donc assurer une ventilation suffisante. En outre, il est recommandé de ne pas faire fonctionner les composants à proximité des puissances dissipées maximales autorisées, car c'est justement dans ce cas que l'on peut s'attendre à ce que le composant lui-même génère beaucoup de chaleur.

Le coefficient de température (appelé valeur TK) est indiqué comme mesure de la variation de la valeur de résistance. La valeur est spécifiée en unités de ppm / ˚C (ppm = parties par million, 1 ppm = "1 millionième" de la valeur totale). Si une valeur TK de ±50 ppm / °C est spécifiée pour une résistance, la résistance varie au maximum du facteur multiplicatif ±0,000050, c'est-à-dire de "50 millionièmes" de la valeur totale, en cas de variation de température de 1°C. Supposons qu'un composant ait une valeur de résistance spécifiée de 1 MΩ. Alors, lorsque la température augmente ou diminue de 1°C, la valeur de résistance spécifiée peut varier jusqu'à 50 Ω, c'est-à-dire qu'elle peut diminuer ou augmenter jusqu'à 50 Ω. En général, on peut utiliser la formule suivante :
RT=Rref *[1+TK*(T-Tref)] OùTref...température de référence (généralement 20°C, parfois 0°C ou 25°C) Rref...résistance de référence TK...coefficient de température T... Température de service RT...Valeur de la résistance en service
Cela s'applique à l'exemple du texte ci-dessus :Tref = 20°C Rref = 1 MΩ = 1 000 000 Ω TK = ±50 ppm / °C = ±0,000050 / °C
La formule donne les valeurs suivantes pour des variations de 1°C et 10°C : R(T=20°C) = 1 MΩ * [1 ± 0,000050 * (20 - 20)] = 1 MΩ * [1 ± 0] = 1 MΩ R(T=21°C) = 1 MΩ * [1 ± 0,000050 * (21 - 20)] = 1 MΩ * [1 ± 0,000050] = 1 000 000 Ω ± 50 Ω R(T=40°C) = 1 MΩ * [1 ± 0,000050 * (40 - 20)] = 1 MΩ * [1 ± 0,001000] = 1 000 000 Ω ± 1000 Ω
Nous ne proposons dans notre portefeuille que des résistances de qualité qui présentent une stabilité et un comportement à long terme significativement meilleurs, qui permettent des tolérances de résistance nettement plus étroites et des valeurs de résistance plus précises que les résistances standard. Nous nous concentrons sur les résistances de précision.
Résistance de puissance, résistance de mesure, diviseur de tension ou thermistance, il s'agit souvent de composants très individuels et spécifiques au client. Grâce à notre "Resistor Engineering", nous vous conseillons volontiers et trouvons pour vous la solution produit optimale ; et celà déjà à partir de quantités relativement faibles.
Nous sommes votre partenaire pour des produits de qualité assurée. Avec une grande fiabilité de livraison, nous parions sur des partenariats à long terme et vous accompagnons pendant toute la durée de vie de votre application. Notre ambition est de fournir à chaque client, de manière tout à fait individuelle, le meilleur résultat fonctionnel et économique. Un paquet complet répondant exactement à vos besoins. C'est notre devise depuis plus de 60 ans.
 EN
EN DE
DE ES
ES FR
FR PT
PT IT
IT


































